Complex is een veel gebruikt woord.
23-6-2022
Complexiteit, klimaat, CO2 en ingenieurs – Inleiding voor aspirant klimatologen
Een bijdrage van Kees le Pair.
Complexe systemen hebben meer dan één actor, die elkaar beïnvloeden. Om ze vanuit één dominante actor te begrijpen, moet aan voorwaarden voldaan zijn. Ook als die actor zelf goed begrepen is, leidt dat in complexe systemen tot onverwachte uitkomsten.
Een planeetbeweging dient tot voorbeeld. De toets van atmosferisch CO2 begrip, temperatuur begrip en begrip van hun onderlinge relatie, aan die voorwaarden is negatief. Enig begrip is uit praktijkonderzoek aan het totale systeem af te leiden. Ingenieurs, medici en andere vakmensen doen dat al eeuwen.
Inhoud
- Complexiteit
- Planetenbeweging
- Klimaat
- Temperatuur
- CO2
- CO2 en temperatuur
- Conclusie CO2-temperatuur
- Discussie en Ingenieurs
- Dank
- Noten
1. Complexiteit
Complex is een veel gebruikt woord. Het heeft verschillende betekenissen(1). In natuurlijke processen is er een eenduidige omschrijving:
Een complex systeem wordt beheerst door verschillende elkaar wederzijds beïnvloedende actors.
Klimaat is zo’n systeem evenals het opslag- en transportsysteem van CO2. (Ook talloze andere systemen zijn complex.)
Een complex systeem kunnen wij soms beschrijven uitgaande van een of enkele van de actoren. Althans indien aan zekere voorwaarden is voldaan. Later in dit artikel betoog ik dat dat bij het klimaat en CO2 niet het geval is (2) en hoe wij met zoiets kunnen omgaan.
- De gekozen actor moet nauwkeurig bekend zijn.
- Het effect van de werking van die actor op het totale systeem moet substantieel zijn t.o.v. de ruis veroorzaakt door de overige actors.
- De begincondities, d.w.z. de toestand waarin het systeem bij aanvang verkeerde, moeten nauwkeurig bekend zijn.
- De beschrijving van een dynamisch proces moet rekening houden met procestijden. (Vaak voldoen (evenwichts) thermodynamische beschouwingen niet aan die eis.)
Feynman leerde ons:
Wanneer niet aan a) is voldaan leiden accurate en zeer doordachte mathematische berekeningen tot idiote uitkomsten.
Dat geldt ook voor de andere condities.
Gemakshalve omzeilen we het probleem vaak door te veronderstellen dat behalve één alle andere actors constant zijn en dat het systeem dan wel met die ene actor kan worden beschreven. Dat is mis ! Ook dan doen die andere mee. Dat kan zeer contra-intuïtieve resultaten geven.
Omdat dit nogal abstract lijkt, geef ik een concreet voorbeeld.
2. Planetenbeweging.
Tycho Brahe bracht nauwkeurig met zijn instrumenten zonder spiegels of lenzen de planetenbeweging in kaart. Johannes Kepler leidde daaruit beschrijvende wetten af. En Isaac Newton Newton verklaarde dat alles uit de wederzijdse aantrekking van twee massa’s. Het bleek dat de daarmee berekende beweging van de aarde om de zon aardig met de waarnemingen klopte, maar niet precies. Dat kwam doordat ook de maan en de andere planeten de aarde aantrokken. Dus probeerde men “even” de beweging te berekenen voor drie in plaats van twee massa’s. Dat lukte echter niet. Newton’s differentiaalvergelijkingen kunnen daarvoor principieel niet worden opgelost.
Meer massa’s verergeren het probleem. We kunnen het wel numeriek. D.w.z. Uitgaande van de begin toestand berekenen we een klein stapje onder invloed van alle krachten en vervolgens rekenen we opnieuw met de uitkomst van de vorige berekening als begin, de volgende uit … enz.. We noemen dat iteratie. Met hulp van moderne computers kun je zo met steeds kleinere stapjes en heel veel iteraties met een bepaalde zekerheid de toekomstige toestand berekenen. Maar niet precies! Het is wel voor veel doeleinden nauwkeurig genoeg.
Toch klopte het niet helemaal binnen de berekende nauwkeurigheid, toen men nog beter kon meten. Het verschil tussen metingen en de berekening bij Mercurius bracht aan het licht dat er iets mis was met voorwaarde a). Het sub-proces van attractie tussen twee massa’s van Newton. Einstein’s relativiteitstheorie bracht dat in het reine. Nu kunnen we het daardoor goed, mits numeriek en we voldoende vaak itereren.
Let wel. Hier hebben we te maken met een systeem waarvan het sub-proces – de beweging van twee massa’s – exact bekend is, evenals de begintoestand. Zo voorspellen we tegenwoordig planetenbewegingen. Kortgeleden deden onderzoekers dit voor Mercurius. Ze berekenden haar positie na een lange tijd. Vervolgens herhaalden ze de berekening voor dezelfde periode met dezelfde iteratie. Ze kozen alleen een 2 cm verschoven begin positie van Mercurius. De uitkomst van de eerste berekening leverde een positie op een punt nagenoeg op de thans bekende baan van die planeet. De tweede berekening echter leerde dat Mercurius zich op dat tijdstip in de zon zou bevinden. Een twee cm veranderde beginpositie is op kosmische afstanden natuurlijk verwaarloosbaar. Maar het gevolg van het minieme verschil is voor dit complexe systeem dramatisch anders. N.B. de foutenmarge als gevolg van de iteratie was de onderzoekers bekend en naar we mogen aannemen, klein genoeg in vergelijking met de 2 cm. Vandaar de eerste uitkomst. Maar 2 cm “fout” in de begin toestand maakt in dit simpele complexe systeem een miljoenen malen groter verschil in de eindtoestand.
Hoe kan zo’n klein verschil in een afzienbare tijd uitgroeien tot zo’n kosmisch drama? 2 cm verschuiving brengt die planeet heus niet morgen in botsing met de zon. Indien door die verschuiving de interactie met zijn actoren iets verschilt, is de invloed van alle actoren actoren anders. Ook die van de actoren, die we voor het gemak constant hielden.
Een berekening van het gedrag van een systeem bestaande uit nauwkeurig bekende subsystemen noemen we fundamenteel of ‘based on first priciples‘. We nemen zelfs genoegen als het alleen numeriek kan, omdat we dan de foutenmarge in het eindresultaat kunnen aangeven.
In de werkelijke wereld voldoen complexe systemen zelden volstrekt aan alle genoemde condities. Toch kan je dan soms het systeem op basis van ‘first principles‘ redelijk beschrijven, mits bij benadering aan de condities is voldaan. De onzekerheid wordt wel veel groter dan alleen door de numerieke methode, zoals we zagen in het planetenvoorbeeld.
Indien voorwaarde b) kleiner is dan half de ruis, zegt de berekening minder dan een wegwijzer, die vertelt: een van deze wegen leidt naar uw bestemming.
De sterrenkunde kent nog talloze aan complexiteit te wijten onzekerheden. Prof. E. v.d. Heuvel, astrofysicus, noemde als voorbeelden de stermodellen(3). Ook daar zijn vele actors. Centraal staan daarin vier gekoppelde differentiaalvergelijkingen. (Veel minder dan in klimaatmodellen.) En de randvoorwaarden zijn redelijk goed bekend. “Na meer dan vijftig jaar onderzoek op dit gebied hebben we nu redelijk goede (numeriek berekende) stermodellen voor sterren van allerlei soorten massa’s. Toch begrijpen we lang nog niet alles.” Hij noemt voorbeelden en voegt eraan toe: “Dit stermodellen-probleem is veel eenvoudiger dan dat van de klimaatmodellen. Daarbij heb je veel meer differentiaalvergelijkingen en zijn veel van de randvoorwaarden lang niet zo duidelijk als bij de stermodellen”.
3. Klimaat
Klimaat is een vaag begrip. Het staat voor een gemiddelde weertoestand en verschilt voor elke plaats op aarde. Weer is een grote verzameling verschijnselen zoals temperatuur, luchtdruk, vochtigheid, wind, neerlag enz. Plaatsen op aarde met eenzelfde gemiddelde temperatuur, kunnen heel erg verschillen in gemiddelde wind of neerlag enz. en in verdeling van die temperatuur over de dag of het jaar. Er is dus niet zoiets als een wereldklimaat. Bovendien gaat het eigenlijk niet om het wereldklimaat, maar om dat van een een deel van een dun schilletje van de aarde, waarin mensen leven(4). En Irakezen beleven klimaat anders dan Inuïts.
Discussie is daarom alleen zinvol over meetbare verschijnselen, als temperatuur, zeeniveau e.a., samenstelling van zee, lucht en bodem en bovenal zongedrag. Het systeem waarin ze een rol spelen is uiterst complex. Beschrijvingen moeten dus voldoen aan de voorwaarden voor complexe systemen.
Een spraakmakende samenhang is de relatie tussen temperatuur en atmosferisch CO2. Elk voor zich ook weer een complex systeem, waarover bibliotheken vol zijn geschreven. Daarin is niet altijd goed gelet op voorwaarden, waaraan beschrijving van een complex systeem moet voldoen.
4.Temperatuur
Planeten ontvangen stralingsenergie van de zon. Zij bevatten zelf chemische en nucleaire energie evenals moleculaire bewegingsenergie, die wij als temperatuur meten. Het eenvoudigst denkbare planeet systeem is een bol die een nagenoeg cirkelvormige baan om de zon beschrijft en zelf geen inwendige energie heeft. Die moet in stationaire toestand de van de zon ontvangen energie weer verliezen aan het heelal. Dat doet hij d.m.v. warmtestraling. Na aftrek van reflectie – gereflecteerde straling gaat ongebruikt direct terug de ruimte in – moet die bol daarom een temperatuur (hoger dan 3 K(5)) hebben. Omdat de zon de bol niet overal even sterk beschijnt en aan de nachtkant helemaal niet, verschilt de geabsorbeerde energie van plaats tot plaats. Dus ook de temperatuur die daar nodig is om die energie weer kwijt te raken.
Het proces kent twee uitersten. Het ene is dat de bol zelf niets doet om de temperatuur gelijkmatig over zijn oppervlak te verdelen. In dat geval heeft elke plek aan het oppervlak op elk moment precies die temperatuur, die nodig is om de zonne-energie op die tijd ook weer kwijt te raken.
In dat geval is onder aardse stralingsomstandigheden de temperatuur gemiddeld over het oppervlak 145 K(6) (-128 °C) Het andere uiterste is een bol, die voortdurend de binnenkomende energie gelijkmatig over zijn oppervlak verdeelt, d.w.z. overal steeds dezelfde temperatuur heeft. In dat geval is de over het oppervlak heersende temperatuur overal steeds 255 K(6) (-18 °C).
Planeten zijn echter complex zij uniformeren de temperatuur slechts gedeeltelijk. Een deel van de uniformering geschiedt door rotatie om hun as. Een deel van de overdag ontvangen energie belandt op een andere plaats, voor het is uitgestraald. Indien ze een atmosfeer hebben, waarin het waait, en oceanen die stromen uniformeren die eveneens. Deze processen zijn net als de mate van reflectie aan verandering onderhevig, waardoor de energiestromen verre van uniform in de tijd zijn en van plaats tot plaats verschillen. Daarom leert deze simpelste van alle verklaringen voor de aardse stralingsevenwicht temperatuur een onbekende gemiddelde straling evenwicht temperatuur op ergens tussen 145 en 255 K(7).
Meteorologen refereren vaak naar een gemiddelde temperatuur van het bewoonbare deel van onze aardschil, die zij afleiden uit plaatselijke satelliet- of andere metingen. Die is omstreeks 288 K (+15 °C). Dat kan dus niet onze stralingsevenwicht temperatuur zijn. Het verschil met de maximum-evenwichtstemperatuur noemt men het broeikaseffect, als gevolg van het accumuleren van energie voor het wordt uitgestraald. Dat wordt vaak toegeschreven aan zgn. broeikasgassen in de atmosfeer, w.o. CO2. (Waterdamp doet meer.)
Omdat we weten dat de temperatuur niet uniform is, is de stralingsevenwicht temperatuur < 255 K. Daar er geen sprake is van uniformiteit, moet het broeikaseffect, alles dat hoger is dan de feitelijke stralingsevenwicht temperatuur verklaren. Wij weten nog op geen vijftig graden nauwkeurig, wat de aardse stralingsevenwicht temperatuur is, dus wat de aardse broeikas doet. Hoewel de rotatie van de aarde zo goed als constant is, is de reflectie en de absorptie dat niet. Daardoor is zelfs dat deel van de broeikas niet constant. En de oceaan is belangrijk in het uniformeringsproces door energietransport, Ook dat is variabel. Atmosferisch infrarood absorberend gas, vooral H2O, CO2 en CH4, methaan, beïnvloeden zowel ingaand als uitgaand het stralingsenergie transport. H2O doet dat ook via wolken (reflectie). Verder is er uitstroom door massatransport en fase verandering. Het energietransport is dus een uiterst complex systeem met talloze variërende actors. Dus is de vraag, of de temperatuur, die door een deel van de energiestroom bepaald wordt, fundamenteel – d.w.z. met hulp van ‘first principles‘ te beschrijven is, afhankelijk van de bovengenoemde voorwaarden.
Gelet op de hiervoor genoemde onzekerheden is het subsysteem aards energie transport en dus temperatuurverdeling op geen stukken na goed bekend. Dus geldt daarvoor Feynman’s waarschuwing: accurate en zeer doordachte mathematische berekeningen op basis van ‘first principles‘ leiden tot idiote uitkomsten.
5. CO2
Atmosferisch CO2 krijgt veel belangstelling als actor in het energietransportsysteem van de aarde. Miljarden jaren geleden bestond de atmosfeer voornamelijk uit CO2, 500 miljoen jaar geleden was dat nog maar 0,5 % (5000 ppM). In de laatste 400.000 jaar tijdens hoogtepunten van vier interglacialen was het nog 0,03% (300 ppM) en thans 0,042% (420 ppM). Aan het eind van de laatste ijstijd was het nog slechts 0,018%(8). CO2 is niet geconserveerd. De hoeveelheid verandert door chemische omzetting; het lost op in water, wordt door bacteriën en planten omgezet in andere chemische stoffen die het deels later weer in circulatie brengen. Mensen doen dat ook. Die geven de natuur een deel van de CO2 terug. Insecten doen dat beter, die brengen jaarlijks tien keer zoveel CO2 in de lucht als de mens met al zijn machines.
De talloze processen die CO2 uit de lucht halen, of toevoegen hebben alle hun eigen procestijd. CO2 opgelost in de oceaan, dissocieert in de mate die afhankelijk is van temperatuur en saliniteit. Een deel wordt omgezet in carbonaten, kalk en rotsen, Die ook weer ontgassen. Dergelijke processen hebben procestijden van miljoenen jaren, vele millennia, en eeuwen. Er zijn ook processen die veel korter duren. Een boom die een blad vormt, dat ’s winters verliest, waarna het verrot, haalt daarmee binnen een jaar evenveel CO2 uit de lucht als hij er weer in stopt. Bouwt hij er takken van of zijn stam, dan kan hij het tientallen jaren tot eeuwen vasthouden. En als die stam na omvallen onder de grond raakt en de natuur er steenkool uit maakt, kan het wel langer dan 100.000 jaar duren voor iemand er weer atmosferisch CO2 van maakt en aan de lucht teruggeeft.
Ook het binnenste van de aarde bevat koolstof-houdende verbindingen, die via vulkanen gestaag of incidenteel in de vorm van CO2 in de lucht belanden.
Het Global Carbon Project is een groot internationaal samenwerkingsverband van onderzoekers, dat probeert het CO2 systeem, opslag, transport en omzetting in kaart te brengen(9). Het accent ligt op de invloed van de mens. Het project stuit op complexiteit. Het voldoet nauwelijks aan een van de gestelde voorwaarden. En veel van het onderzoek is gericht op een of enkele van de hiervoor aangeduide sub-processen. Voor echt begrip van de koolstof opslag en beweging, uit zulke gebrekkige sub-proceskennis is dus geen enkel hoop. Wat overigens niet wil zeggen, dat er geen fenomenologische kennis van het systeem kan worden verkregen voor een beperkte periode.
Dr. A. Huijser en ik deden dat voor de atmosferische CO2 hoeveelheid en het CO2 afkomstig van fossiele brandstof(10). Wij pretenderen niet het systeem te begrijpen. We hebben slechts laten zien dat vanuit data van de door de mens verbruikte koolstof met een precisie van ~1 ppM de atmosferische concentratie kan worden berekend in de periode 1880 – 2020. Aan een voorspelling over een periode langer dan de volgende 60 jaar wagen we ons niet van wege de complexiteit van het systeem.
De CO2-, of beter de koolstofhuishouding van de aarde blijft nog heel lang een raadsel. En fundamenteel begrip, uitgaande van alle sub-processen is niet in zicht.
6. CO2 en temperatuur
CO2 in de atmosfeer absorbeert infrarode straling, zendt het zelf in alle richtingen uit en verwarmt daarmee de aarde. Het grootste deel van de geabsorbeerde stralingsenergie zet het om in warmte. Die warmte belandt goeddeels in de bewoonde schil. Ziedaar de invloed van CO2 op de temperatuur; die de samenleving onrustig maakt.
Natuurkundig bezien is deze bewering zonder betekenis zo lang er geen getallen aan hangen. Getallen zijn er genoeg, zowel over wat CO2 doet om de stalingsevenwicht temperatuur te brengen tot de huidige waarde in die woonschil, als over wat meer of minder CO2 betekent voor de verandering van de huidige temperatuur. De uitkomsten van al die studies verschillen drastisch onderling. De oorzaak van die verschillen is de complexiteit van het systeem. De ene studie kent iets meer gewicht toe dan de andere aan een of ander meetellend subsysteem of aan de effectiviteit van het CO2 in de atmosfeer zelf.
Omdat er talloze andere actors zijn dan atmosferisch CO2 is dit weer een kwestie van de invloed van een ervan op het gedrag van het systeem zelf. De actoren beïnvloeden ook elkaar, het is dus een complex systeem in optima forma(11). En we moeten dus nagaan of een uitleg aan de complexiteit voorwaarden voldoet.
Bij voorwaarde a) gaat het over de nauwkeurigheid waarmee het begrip van het subsysteem van deze actor zelf bekend is. Daaraan is dus niet voldaan, gezien de verschillende uitkomsten van de studies. Een tegenargument, dat al die studies op een-na fout kunnen zijn en wanneer we de goede zouden gebruiken, we dit subsysteem dus wel goed kennen, vindt geen aanhang bij de meerderheid van de klimatologen en in het IPCC, het internationale klimaatpanel.
Dat publiceert een spreiding van 2 – 8 °C voor een onzekere CO2 toename tot het eind van deze eeuw. Prof. W.J. Witteman komt niet hoger dan enkele tienden van een graad bij CO2 verdubbeling(12) (!). Die onzekerheid voor een systeem dat in anderhalve eeuw 1,3 °C in temperatuur is gestegen is te groot om CO2 als volledig bekende actor te accepteren.
Voorwaarde b) vergt een significante bijdrage van het subsysteem in de ruis van alle samen. De grootte van de ruis in de gemeten temperatuur, hangt af van de periode en de plaats, waarover men instantane, lokale temperatuurmetingen middelt. Plaatselijk kennen we dag en nacht verschillen van 50 °C. De onzekerheid over miljoenen jaren als gevolg van ideale temperatuurverevening dan wel helemaal geen temperatuurverevening heeft een spreiding van 110 °C. Zelfs als het aandeel van de aardrotatie in de verevening mag worden afgetrokken, resteert een ruis van ca. 50 °C. Bij middeling over tientallen jaren laten de ijskernmetingen een ruis van 12 °C zien in de afgelopen 400.000 jaar. Maandgemiddelden van onze woonschil tonen een spreiding van ~0,5 °C. (Zie de satellietmetingen over de periode 1970 – 2022 in figuur 1. Ook jaargemiddelden fluctueerden in die periode in die grootte.
Fig. 1
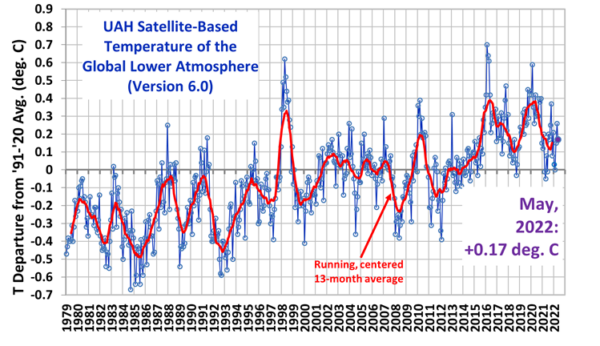
Figuur 1. Maandelijkse en jaarlijkse temperatuur variatie t.o.v het gemiddelde over de periode.
De ‘first principle’ berekeningen van de invloed van CO2-invloed op de temperatuurverandering gaan over “het klimaat”, waarvoor klimatologen afspraken een periode van 30 jaar te kiezen. Zij zijn dus slechts significant, indien CO2 als actor nauwkeurig bekend zou zijn. Bij de onder a) beschreven onnauwkeurigheid, is dat zeker niet het geval.
Voor de verandering van de temperatuur in een korte, achter ons liggende periode is dat anders. Die is vanaf 1979 redelijk bekend. Vanaf dat jaar zijn er berekeningen over de CO2-invloed in beeld gebracht door John Christy en Roy Spencer in figuur 2.
Fig. 2
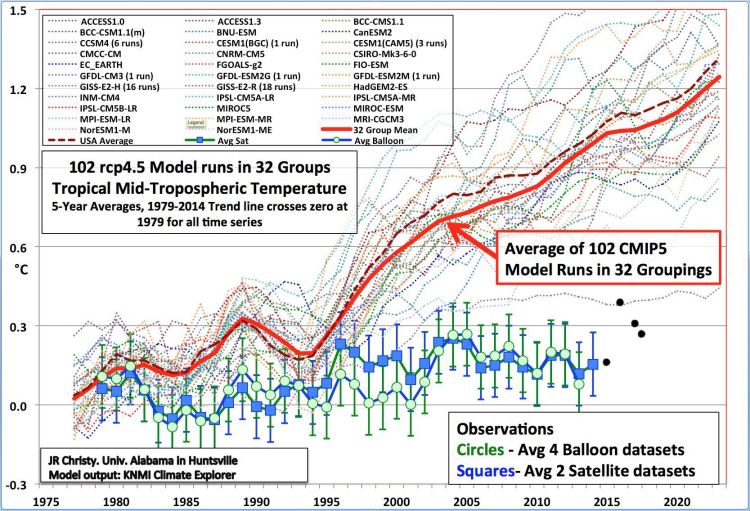
Figuur 2. J. Christy: Gestippelde lijnen geven de ‘first principle’ berekeningen van de temperatuurverandering als gevolg van verandering in concentratie van atmosferisch CO2 sinds 1979 en de gemeten data(13).
Ook bij redelijk bekende begincondities wijken de ‘first principle‘ berekeningen na dertig jaar al significant af van de waarnemingen. (Niet voldaan aan a)) Bekende begincondities helpen zelfs niet bij begrip van temperatuurveranderingen.
Aan voorwaarde d), procestijden en niet-evenwichtsituaties, voldoen sub-proces CO2-temperatuur berekeningen niet. Men rekent met de actuele concentratie(14) en let niet op de tijd, die het zou duren voor de temperatuur van de woonschil zich aan die waarde heeft aangepast. De procestijd voor het instellen van een evenwichtssituatie voor de CO2-concentratie is 53,5 jaar. (Een exces concentratie halveert in 37 jaar.). Hoelang zou het duren voor bv. de oceaan in de woonschil zijn CO2 evenwichtstemperatuur behorend bij 420 ppM heeft bereikt? In niet evenwichtssituaties zijn thermodynamische berekeningen invalide(15).
7. Conclusie CO2-temperatuur
Onze kennis van complexe systemen rechtvaardigt geen valide uitspraken op grond van de invloed van de actor atmosferisch CO2 op de temperatuur van de woonschil. Er is noch aan de vereiste voorwaarden voldaan voor de temperatuur, noch aan die voor de temperatuurverandering over perioden van menselijke maat. Daarom leiden zeer doordachte mathematische berekeningen tot idiote uitkomsten.
8.Discussie en Ingenieurs
Ingenieurs en vele anderen die uitspraken over systemen doen, doen dat over complexe systemen, op grond van een enkele actor. Hoe fout dat kan zijn, zelfs bij een kleine onnauwkeurigheid in actor kennis, zagen we in het planetenvoorbeeld. Ingenieurs weten dat en hebben daarvoor een listige aanpak. Zij berekenen eerst met precieze natuurkundige kennis, wat hun systeem gaat doen. Dan bouwen ze het en gaan kijken wat het in de praktijk doet. Als dat anders is dan bedoeld, veranderen ze een kleinigheid en kijken opnieuw, net zo lang tot ze het zo hebben gemodificeerd, dat het waarschijnlijk voor de benodigde tijd, goed zal voldoen.
Ik geef een voorbeeld. In een machine is een hefboom nodig. We weten precies welke krachten bij een bepaalde lengte passen om het ding in evenwicht te houden, c.q. te laten bewegen. Indien de machine niet doet, wat hij zou moeten doen, olieën we de lagering, of maken de hefboom robuster om doorbuiging te voorkomen, of we veranderen de lengten verhouding. Net zo lang tot het systeem werkt. Vaak wijkt het daarna danig af van het aanvankelijke ontwerp. Soms blijkt dan echter, dat het systeem helemaal niet kan, wat het moet. En helpt ook dit gefoezel(16) niet. Bij schepen met rader-voortstuwing bijvoorbeeld. Veranderingen aan de raderen en de motor hielpen niet voor snellere schepen en in zeegang. Tenslotte ging het systeem overboord en gingen we over op een nieuw, met propellers of turbines. Pas praktijk tests leren of je iets hebt aan de first principle aanpak.
Met gefoezel(16) trachten klimatologen de ‘first principle‘ aanpak van het CO2-temperatuur systeem passend te maken op de waarnemingen. Dat het hen niet is gelukt, zien we in figuur 2. Complexiteitsvoorwaarden, maken echter die hele aanpak uitzichtloos. Daarom zit er, voor wat de temperatuur van de woonschil betreft niets anders op, dan zien of uit patronen van de systeemwaarnemingen iets met redelijke waarschijnlijkheid is te concluderen. Zo ging het al eeuwenlang bij ingenieurs artsen, en andere vakmensen.
Ook het KNMI leidt de afhankelijkheid van de temperatuur van CO2 af uit patronen van gemeten temperatuur- en CO2-concentratie reeksen. Praktijkgegevens dus. Het instituut oordeelde de samenhang zo sterk, dat het daarmee kwantitatieve voorspelingen deed. De door het Instituut gebruikte methode van statistische analyse werd echter al in 1924 op grond van wiskundige statistiek ondeugdelijk bevonden. Die zou met evenveel recht de SP500-index aanwijzen als veroorzaker van de temperatuurstijging. Maar een temperatuur afhankelijk van de prijs waarop mensen aandelen verhandelen, is niet geloofwaardig. Op praktijk patronen afgaan is dus wel sterk afhankelijk van de wiskundig-statistische bekwaamheid van de onderzoekers(17).
Doen we het voor de temperatuur in onze woonschil, dan zouden we voorlopig moeten rekenen op basis van simpele trendanalyses met een temperatuurstijging van ~1 °C/eeuw. Voor de zeespiegelstijging ~2 mm/jaar. Enzovoorts. Op andere verschijnselen zoals frequentie en kracht van orkanen, hittegolven, overstromingen, vulkaanuitbarstingen enz. is geen pijl te trekken. Uitspraken daarover horen thuis in de sfeer van waarzeggers en profeten.
9.Dank
Met dank aan Dr. A. Huijser, Prof. C.A. de Lange, Prof. W.J. Keller, Prof. E. v.d. Heuvel voor commentaar, verbeteringen, correcties en aanmoedigingen.
***.
10. Noten
- Het zwembad in mijn woonplaats bv. heet “Sport- en Evenementencomplex”.
- KNMI en IPCC gaven blijk de kritiek te kennen, al camoufleerden ze dat effectief:
KNMI:
“The variability of the system poses limitations to the predictability of the climate state. Internal variations of the climate system beyond monthly time scales apart from the contribution from the positive multidecadal surface temperature trend that is currently eminent (Oldenborgh et al. 2012) and oceanic variability (Hazeleger et al. 2013), are difficult to predict and at time scales of 30 – 100 years useful predictions are basically impossible. Not only because of the large contribution of the natural variability, also because the external forcing related to human activity is considered to be unpredictable. Any attempt to make climate predictions at a relatively small spatial scale such as the Netherlands or even Western Europe for multiple decades ahead cannot be expected to lead to skilful results. KNMI
IPCC:
“Scenarios are images of the future, or alternative futures. They are neither predictions nor forecasts. Rather, each scenario is one alternative image of how the future might unfold. A set of scenarios assists in the understanding of possible future developments of complex systems. Some systems, those that are well understood and for which complete information is available, can be modeled with some certainty, as is frequently the case in the physical sciences, and their future states predicted. However, many physical and social systems are poorly understood, and information on the relevant variables is so incomplete that they can be appreciated only through intuition and are best communicated by images and stories. Prediction is not possible in such cases”. (IPCC, 2007) - E. v.d. Heuvel ,priv.com.”… ik heb mijn skepsis over die klimaatmodel-berekeningen. In mijn vak de astrofysica maken we modelberekeningen van sterren. We hebben daar vier gekoppelde differentiaalvergelijkingen als basis, en kennen de randvoorwaarden redelijk goed (druk en temperatuur aan de buitenrand van de ster zijn in goede benadering nul (de temperatuur niet helemaal, maar in vergelijking met die in het centrum wel), en in het centrum zijn de massa en de lichtkracht nul, dus we hebben vier bekende randvoorwaarden). Verder hebben we een hele hoop fysica nodig: kernreacties, transport van energie door convectie of transport door absorptie en re-emissie, absorptiecoëfficiënten bij allerlei temperaturen en drukken en chemische samenstellingen (veel ervan berekend in Los Alamos voor atoombommen), enz., enz,. Na meer dan vijftig jaar onderzoek op dit gebied hebben we nu redelijk goede (numeriek berekende) stermodellen voor sterren van allerlei soorten massa’s. Toch begrijpen we lang nog niet alles, bijvoorbeeld het sterke massaverlies (door sterrenwinden) dat je bij zware sterren van grote lichtkracht ziet gebeuren. En modellen voor koele sterren (rode reuzen) waarin veel moleculen optreden in de buitenlagen, zijn nog steeds heel problematisch, evenals voor rode dwergen. Dit stermodellen-probleem is veel eenvoudiger dan dat van de klimaatmodellen. Daarbij heb je veel meer differentiaalvergelijkingen en zijn veel van de de randvoorwaarden lang niet zo duidelijk als bij de stermodellen: veel van de randvoorwaarden (bijv. oceaantemperatuur als functie van geografische breedte, hoeveelheid sneeuwoppervlak, enz.) zijn variabel. Ik ben geen expert op dit gebied, maar mijn gevoel is dat die modellen aanzienlijk onzekerder moeten zijn dan onze stermodellen, die eigenlijk relatief eenvoudig zijn, en ons toch nog steeds ook voor problemen stellen.
(ClP: Prof.Van den Heuvel denkt overigens dat CO2 een belangrijke factor in temperatuurstijging is. De CO2-concentratie is duidelijk hoger dan in vorige interglacialen. De temperatuur niet, maar die stijgt nog wel, ongeveer 1 °C/eeuw Niet 4 °C in 80 jaar, wat het IPCC beweert. - De temperatuur in het binnenste van de aarde loopt op tot 6000 °C. Aan het oppervlak op hoge breedten kan het -50 °C zijn en op 15 km hoogte ook met daartussen weer +10 °C.
- Aannemend dat we aan de ons omringende ruimte een temperatuur van 3 K (-270 °C) mogen toeschrijven.
- Data en berekening van gemiddelde stralingsevenwicht temperaturen als functie van reflectie en emissiviteit: §4, Bol, webstek.
- De Maan en de aarde hebben weliswaar een vergelijkbare stralingsomgeving, maar zijn onderling onvergelijkbaar. Albedo en emissiviteit verschillen. Op de maan ontbreken oceaan en atmosfeer en de rotatiesnelheid is 28 maal zo laag. De maximum temperatuur is er 400 K (+127 °C) en de laagst gemeten temperatuur is er 25 K (-248 °C). Het heeft geen zin daaruit conclusies te trekken voor de gemiddelde stralingsevenwicht temperatuur van de aarde
- 180 ppM (0,018%) 20.000 jaar geleden was gevaarlijk laag, omdat planten bij 150 ppM niet of nauwelijks nog groeien. Veel leven o.a. het onze, is daar onder niet meer mogelijk.
- Global Carbon Project.
- Dr. A. Huijser en ik hebben bv. de CO2 voorraad in de lucht, die sinds 1960 dagelijks op Mauna Loa gemeten wordt, vergeleken met het CO2 dat door mensen uit fossiele brandstof in de lucht werd gebracht. Het bleek dat in de periode 1960 – 2020 de natuur, geleidelijk een groeiend een deel van die toename, weer ongedaan maakte. Wij vonden dat in die periode bij een atmosferische concentratie van 287 ppM de natuur ongeveer evenveel CO2 jaarlijks toevoegt als ze er uit haalt. Wij konden ook oudere metingen dan die op Mauna Loa, verklaren, uitgaande van zo’n evenwicht in de periode 1880 – 1960 van 280 ppM. De 7 ppM verschil stemt redelijk overeen met de verminderde oplosbaarheid in zeewater bij iets hogere temperatuur; of de Vostok ijskernmetingen. Wij konden ook een processnelheid afleiden. De exces concentratie boven het vigerende evenwicht zou zonder verdere menselijke toevoeging in 37 jaar halveren. Wij verwachten dat in de periode 2020 – 2080 met een evenwichtsconcentratie van 295 ppM gerekend mag worden. Met 420 ppM actueel, is het exces op dit moment dus 125 ppM. ‘How does CO2 escape’?
- Indien meer CO2 de temperatuur verhoogt, lost CO2 minder goed op in de oceaan, waardoor de CO2 concentratie in de lucht toeneemt, dan wel de afvoer van het exces vertraagt. Meer CO2 vergroent de aarde, waardoor reflectie en absorptie veranderen. Meer CO2 in de hogere luchtlagen verhoogt de uitstraling naar het heelal, wat de energie afvoer vergroot. Een andere temperatuur betekent een andere hoeveelheid waterdamp, een ander en zelfs invloedrijker infrarood absorbeerder, H2O, heeft nog andere energietransport eigenschappen. Enz. de trits is lang.
- W.J. Witteman.
- De zwarte stippen zijn later door mij toegevoegd uit de satellietmetingen.
- Atmosferisch CO2 wordt bv. vaak behandeld met gebruikmaking van de wet van Henry. Die is echter alleen van toepassing bij evenwicht. Dat is er niet. Er is een voortdurende energiestroom en materiestroom met tussentijdse procesverandering (Van oplossing naar bacterie, plant of gesteente en terug). Er zijn steeds gradiënten. Wie zich daarin verdiept moet teruggrijpen op de kruisrelaties van Onsager en op hydro- en gas dynamica, niet op Henry.
- In GCM modellen werkt men voor het CO2 zelfs met zeer fijne tijdoplossing en iteratie, maar daarmee is het hele systeem, wat temperatuur betreft, nog niet in evenwicht. Er is dus niet aan voorwaarde d) voldaan. (Feynman’s “zeer doordachte mathematische berekeningen”.
- Foezelen kan best heel bruikbare resultaten opleveren, maar praktijk uitkomsten moeten dat tonen. Het heeft veel constructies, systemen, producten enz. tot stand gebracht en patiënten het leven gered. Het is niet per se negatief; het betekent alleen dat het niet kwam door ‘ab initio’ berekeningen. Met gefoezel is echter niets te bereiken indien het doel om gegronde redenen niet bereikbaar is. Wie een raket sneller dan het licht wil maken kan foezelen wat hij wil, het zal niet lukken. Net zo is het met temperatuurvoorspellingen als gevolg van CO2.
- Bijlage 2 (na Bijlage 3) van (CLINTEL-KNMI) Aan het licht gebracht door wiskundig statisticus Prof. W.J. Keller e.a. in het kader van wetenschappelijk advies van CLINTEL aan het KNMI. Het instituut volhardt wegens “tijdgebrek” al enkele jaren in zijn foute analyse.
***
Bron hier.



0 reacties :
Een reactie posten